Confounding Variables

Correlation does not imply causation - if we want to know whether a relationship between an exposure and outcome is causal, we must first consider whether any other factors could have had an influence.

Confounders are external factors which cause both the exposure and outcome. For example, there might be a strong correlation between ice cream sales and shark attacks at the beach, but there is no causal relationship here - both of these are more common in warm weather, so the weather is the confounder. To measure the strength of any causal relationship between exposure and outcome, the strength of the relationship between the confounder and the outcome must also be measured by including the confounder as a model input. In a simple model the strength of these effects (\(x_1, x_2\)) could be estimated as: \(Outcome = x_1 \times Exposure + x_2 \times Confounder\)

In the study of causal inference it is common to use directed acyclic graphs (DAGs) to map the causal relationships between variables, which can help to identify confounders. This can be helpful as it is not always clear whether a potential confounder is in fact a confounder, or a mediator, a proxy confounder, or a competing exposure.

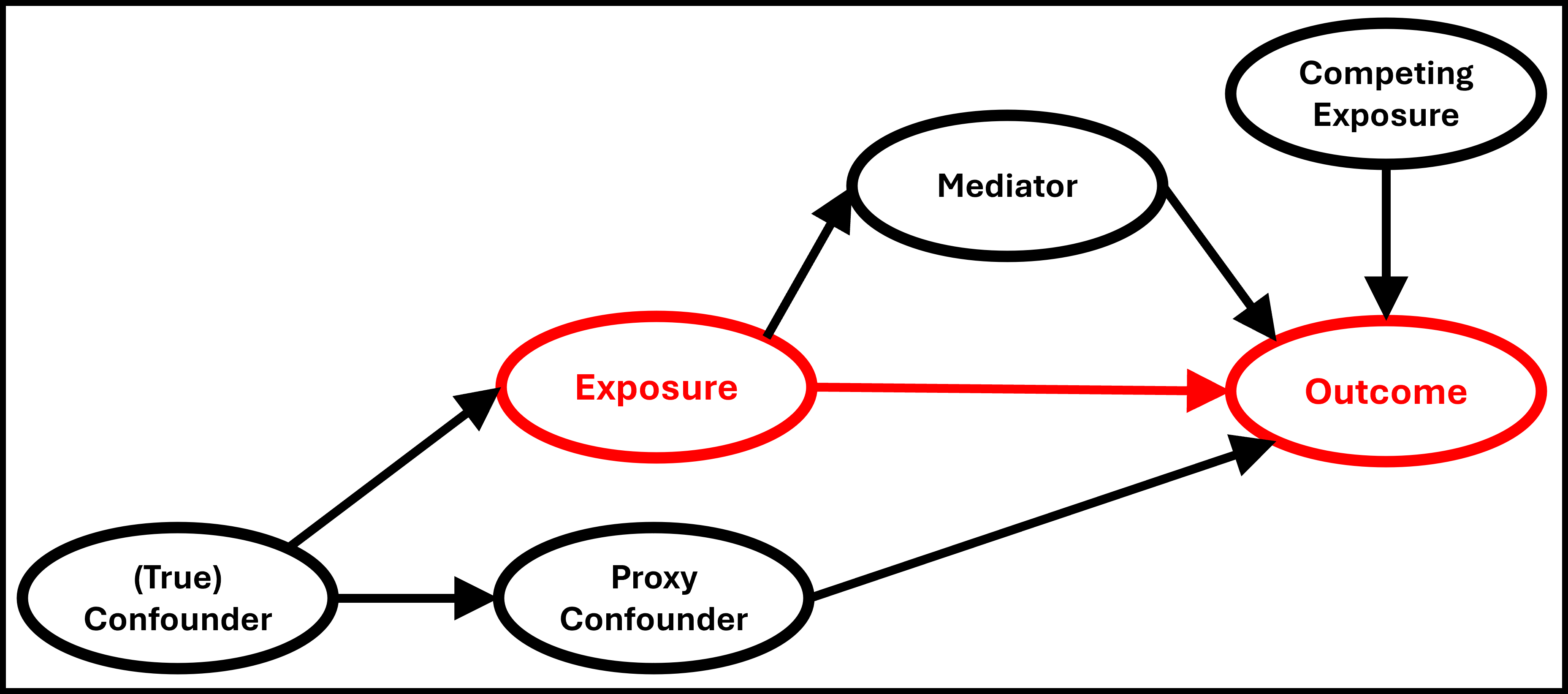
Fig. 91 A directed acyclic graph (DAG), with the relationship of interest indicated in red.

Modelling competing exposures can help to make models more precise, but does not affect modelling bias. Modelling mediators is only required if we wish to estimate the direct causal effect of the exposure on the outcome, rather than the more common total causal effect. True confounders are more informative than proxy confounders, but proxy confounders can offer some information when true confounders are impractical to measure.

In interventional studies, randomly assigning each participant to an exposure group helps to balance out the effects of confounders between the exposure and control groups. This requires a reasonable sample size to work, as if there are very few participants then all of the participants with a specific confounder may be randomly assigned to the same exposure. Randomised controlled trials (RCTs) are frequently used in medical research, and are typically required when assessing the effects of a new drug. When randomisation is not possible, known (measured) confounders can be adjusted for in data analysis, but unknown confounders will still have an impact.